科目代码：602 科目名称：数学
一、考试内容
1、函数和极限
函数的概念及透露表现法，函数的有界性、单调性、周期性和奇偶性，复合函数、反函数、分段函数和隐函数，基本初等函数性子及其图形。
数列极限与函数极限的定义以及它们的性子，无限小和无限大的概念及其关系，无限小的性子及无限小的比较，极限的四则运算，极限存在的两个准则：单调有界准则和夹逼准则，两个紧张极限：
函数延续的概念，函数间断点的类型，初等函数的延续性，闭区间上延续函数的性子(有界性、最大值和最小值定理、介值定理)
2、一元函数微分学
导数和微分的概念，导数的几何意义和物理意义，函数的可导性与延续性之间的关系，平面曲线的切线和法线，基本初等函数的导数，导数和微分的四则运算，复合函数、反函数、隐函数以及参数方程所确定的函数的微分法，高阶导数的概念和求法，一阶微分情势的不变性，微分在近似计算中的应用，洛尔(Rolle)定理，拉格朗日(Lagrange)中值定理，柯西(Cauchy)中值定理，泰勒(Taylor)定理，洛必达(L’Hospital)法则，函数的极值及其求法，函数单调性，函数图形的凹凸性、拐点及渐近线，函数图形的描绘，函数最大值和最小值的求法及简单应用，弧微分，曲率的概念，曲率半径。
3、一元函数积分学
原函数和不定积分的概念，不定积分的基本性子，基本积分公式，定积分的概念和基本性子，定积分中值定理，变上限制积分定义的函数及其导数，牛顿-莱布尼茨(Newton-Leibniz)公式，不定积分和定积分的换元积、分法部积分法，有理函数、三角函数的有理式和简单无理函数的积分，广义积分的概念和计算定积分的近似计算法，定积分的应用。
4、矢量代数和空间解析几何
矢量的概念，矢量的线性运算，矢量的数量积和矢量积的概念及运算，矢量的混合积，两矢量垂直、平行的条件，两矢量的夹角，矢量的坐标表达式及其运算，单位矢量 方向数与方向余弦，曲面方程和空间曲线方程的概念，平面方程、直线方程，平面与平面、平面与直线、直线与直线的平行、垂直的条件和夹角，点到平面和点到直线的距离，球面，母线平行于坐标轴的柱面，旋转轴为坐标轴的旋转曲面的方程，常用的二次曲面方程及其图形，空间曲线的参数方程和一样平常方程，空间曲线在坐标面上的投影曲线方程。
5、多元函数微分学
多元函数的概念，二元函数的几何意义，二元函数的极限和延续的概念，有界闭区域上的多元延续函数的性子，多元函数偏导数和全微分的概念，全微分存在的需要条件和充分条件，全微分在近似计算中的应用，多元复合函数、隐函数的求导法，高阶偏导数，方领导数和梯度的概念及其计算，空间曲线的切线和法平面，曲面的切平面和法线， 二元函数的二阶泰勒公式，多元函数极值和条件极值的概念，多元函数极值的需要条件，二元函数极值的充分条件，极值的求法，拉格朗日乘数法，多元函数的最大值、最小值及其简单应用。
6、多元函数积分学
二重积分、三重积分的概念及性子，二重积分与三重积分的计算和应用，两类曲线积分的概念、性子及计算，两类曲线积分的关系，格林(Green)公式，平面曲线积分与路径无关的条件，已知全微分求原函数，两类曲面积分的概念、性子及计算，两类曲面积分的关系，高斯(Gauss)公式，斯托克斯(Stokes)公式，散度、旋度的概念及计算，曲线积分和曲面积分的应用。
7、无限级数
常数项级数及其收敛与发散的概念，收敛级数和的概念，级数的基本性子与收敛的需要条件，几何级数与p级数以及它们的收敛性，正项级数收敛性的判别法，交错级数与莱布尼茨定理，任意项级数的绝对收敛与条件收敛，函数项级数的收敛域，和函数的概念，幂级数及其收敛半径、收敛区间(指开区间)和收敛域，幂级数在其收敛区间内的基本性子，简单幂级数和函数的求法，函数可睁开为泰勒级数的充分需要条件，ex、sinx、cos x、ln(1+x)和(1+x)α的麦克劳林(Maclaurin)睁开式，幂级数在近似计算中的应用，函数的傅里叶(Fourier)系数与傅里叶级数，狄利克雷(Dirichlet)定理，函数在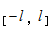
上的傅里叶级数，函数在[0，
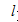]上的正弦级数和余弦级数。
8、常微分方程
常微分方程的概念，微分方程的解、阶、通解、初始条件和特解，变量可星散的方程，齐次方程，一阶线性方程，伯努利(Bernoulli)方程，全微分方程，可用简单的变量代换求解的某些微分方程，可降价高阶微分方程，线性微分方程解的性子及解的结构定理，二阶常系数齐次线性微分方程，高于二阶的某些常系数齐次线性微分方程，简单的二阶常系数非齐次线性微分方程，欧拉(Euler)方程，包含两个未知函数的一阶常系数线性微分方程组，微分方程的幂级数解法，微分方程(或方程组)的简单应用题目。
二、参考书目：
同济大学数学系编, 高等数学（第七版)（上、下）, 高等教育出版社, 2014
科目代码：852 科目名称：计算机组成原理
一、考试内容
第一章 计算机体系概论
1.1 计算机的分类
1.2 计算机的发展简史
1.3 计算机的硬件
1.4 计算机的软件
1.5 计算机体系的条理结构
第二章 运算方法和运算器
2.1 数据与笔墨的透露表现方法
2.2 定点加法、减法运算
2.3 定点乘法运算
2.4 定点除法运算
2.5 定点运算器的组成
2.6 浮点运算方法和浮点运算器
第三章 内部存储器
3.1 存储器概述
3.2 SRAM存储器
3.3 DRAM存储器
3.4 只读存储器和闪速存储器
3.5 并行存储器
3.6 cache存储器
第四章 指令体系
4.1 指令体系的发展与性能要求
4.2 指令格式
4.3 操作数类型
4.4 指令和数据的寻址体例
第五章 中间处理机
5.1 CPU的功能和组成
5.2 指令周期
5.3 时序产生器和控制体例
5.4 微程序控制器
5.5 硬连线控制器
5.7 流水CPU
5.8 RISC CPU
第六章 总线体系
6.1 总线的概念和结构形态
6.2 总线接口
6.3 总线的仲裁
6.4 总线的准时和数据传送模式
第七章 外围设备
7.1 外围设备概述
7.2 磁盘存储设备
7.3 磁盘存储设备的技术发展
7.4 磁带存储设备
7.5 光盘和磁光盘存储设备
7.6 表现设备
7.7 输入设备和打印设备
第八章 输入输出体系
8.1 外围设备的速度分级与信息交换体例
8.2 程序查询体例
8.3 程序停止体例
8.4 DMA体例
8.6 通用I/O标准接口
二、参考书目
1、参考书目：陈书开等主编，《计算机组成与体系结构（第二版）》，武汉：华中科技大学出版社，2010年9月
2、参考教材：白中英主编，计算机组成原理，科学出版社，2008年
